Blog
by Kuntay Celik
Can Residual ML Risk Exceed Inherent Risk? (2)
Diana’s Dilemma
2/21/2025
I will keep this light for your commute at the end of a tiring workday. There is some math in it, but nothing to worry about. It is simple math.
In this chapter, I will delve deeper into our "million-dollar" question with an example and discuss the practical implications of Approach 1 and Approach 2 that were introduced in my earlier write-up. I will use some extreme examples to illustrate the consequences more clearly.
First, let me reiterate that both ML/TF risk assessment and risk-based supervision are complex tasks that should dynamically incorporate various inputs and factors, including the country’s risk context, typologies, and the financial sector’s sophistication. However, there is no harm in starting with a simplified example and focusing on basic principles that can shed light on some foundational aspects. Even the most advanced approaches should incorporate and have responses to these fundamental questions. I want to deepen the discussion step by step in the next chapters. Please bear with me.
Ms. Diana Wise, an experienced bank supervisor in the on-site supervision division, leads a team of 10 bank examiners responsible for three banks (Banks A, B, and C). The team received risk-monitoring scores of Banks A, B, and C from the agency’s off-site supervision division, along with underlying information consistent with these scores. These scores are based on past examinations and ongoing risk-monitoring. As of the exercise date, there are no specific trigger events or red flags affecting the supervision planning.
The off-site supervision division uses a 0 to 100 risk scale for inherent risk, where 0 represents no ML/TF risk, 50 represents a medium level, and 100 represents the maximum level of ML/TF risk. The compliance and effectiveness of AML/CFT controls are reported as a percentage, with 100% representing fully effective AML/CFT controls and 0% represents no AML controls.
- Bank A: A large-scale international bank active in corporate banking, international transactions, private banking, and asset management services. Although recently established, it has rapidly expanded its market share. The supervisory agency’s risk monitoring tool identified an inherent risk score of 85, with an overall AML/CFT control effectiveness of 50%.
- Bank B: A state-owned retail bank focusing on government-to-person and person-to-government payments, other retail products, and financial services to medium and small size enterprises and and innovative start-ups. International transactions are limited. The inherent risk score is 40, with an AML/CFT control effectiveness of 30%.
- Bank C: A microfinance bank serving farmers and merchants. It is a small-scale bank with a limited range of products and almost no international transactions. The inherent risk score is 20, with an AML/CFT control effectiveness of 10% due to staff shortages and manual compliance processes.
Before the new supervision cycle begins, Diana aims to conduct risk-based planning and allocate resources for her team. She seeks assistance from Julia and Marco to develop a preliminary framework for risk-based resource allocation. On purpose, Diana instructs them to work independently at the beginning and try different approaches to develop their analyses. Julia uses Approach 1, while Marco uses Approach 2, resulting in the following:
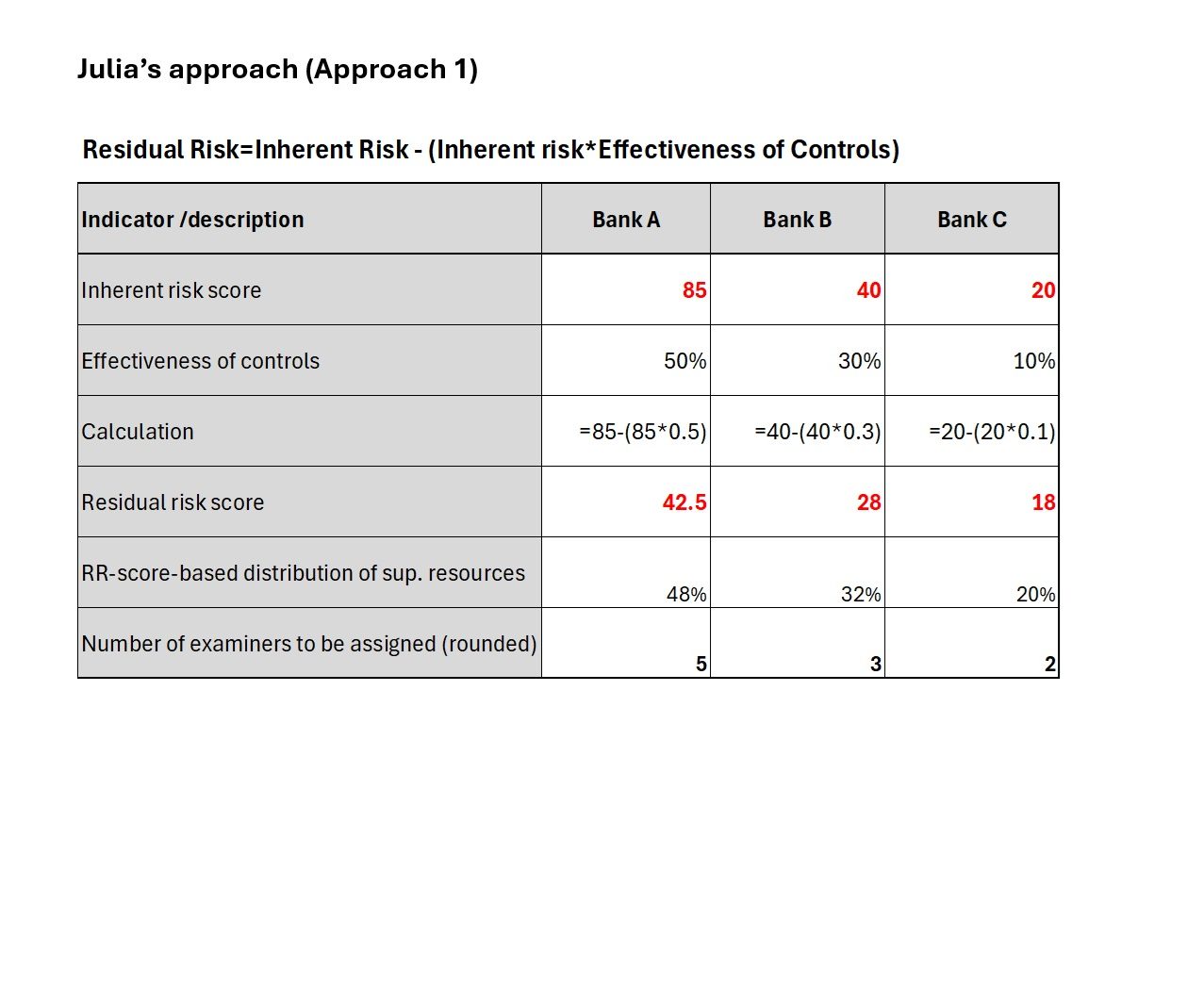
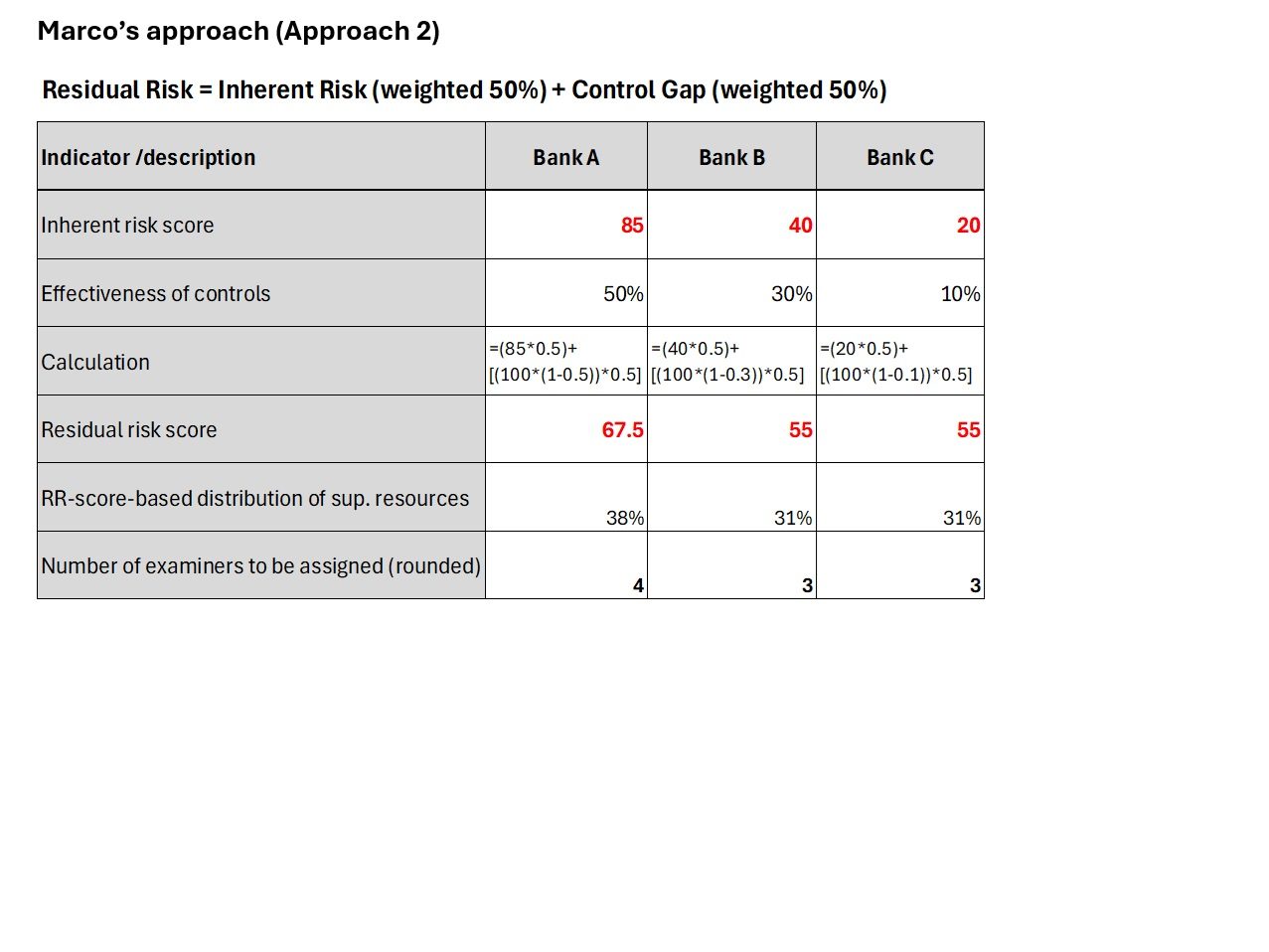
Diana examines both analyses carefully.
In Julia’s approach, the residual risk level is consistently below the inherent risk level. The risk ranking of institutions and the distribution of supervisory resources appear reasonable. However, Bank A's residual risk level (42.5) seems to imply a risk level below medium. This does not seem that accurate given Bank A’s inherent risk profile and 50% effective AML controls. Julia responds by explaining that the Financial Action Task Force’s risk-based approach refers to lower risks and higher risks and, therefore, is about relative risk (i.e., comparing one institution with others in the sector). According to Julia, risk-based allocation of resources should be the focus.
Marco’s approach yields a more realistic residual risk level for Bank A but raises questions, particularly for Bank C. Would a small-scale microfinance bank with limited functions become medium-risk, as risky as a retail bank, due to weaker AML/CFT controls? This result and the implied distribution of supervisory resources do not seem fully intuitive to Diana. Diana notes that this approach penalizes the weak AML/CFT controls by increasing the risk score, and residual risk levels for Banks B and C exceed their inherent risk levels. Carlos admits that some refinements may be necessary but explains that -if not addressed- weaker controls will increase the inherent risk of Bank C; therefore, this approach is more forward-looking. However, Diana thinks Bank C does not have the product diversity needed for money laundering, and its utility for ML purposes is quite limited. She also thinks that if there is such an unusual change in the inherent risk profile of Bank C, this will be red-flagged by the off-site supervision. But she also can see that adjusting the weights may help for more realistic results.
Diana acknowledges the pros and cons of both approaches but finds neither fully reliable. She asks Marco and Julia to improve their approaches so that they have a strong and reliable framework for future supervision planning, especially considering that more financial institutions will be assigned to their team in the medium term.
While Julia and Marco work on their adjustments, please provide any specific advice to help them improve the accuracy and reliability of their models.
To be continued.
Have feedback? I will love to hear from you.
Thoughts on some basic concepts of money laundering and terrorist financing risks:
Can residual risk exceed inherent risk?
In a very recent technical meeting, I had the privilege of diving into an in-depth discussion with a group of seasoned AML/CFT supervisors on some basic concepts of ML/TF risks. In general, I am in favor of being practical in the discussion of AML/CFT matters and cautiously watch the added value of any theoretical discussion. However, discussion and clarity in basic concepts of ML and TF risks are essential matters that can impact the practice significantly. These definitions should serve as a system-wide compass for public and private stakeholders and should have coherent meaning, at least within a national AML/CFT system, if not globally.
Two of these foundational risk concepts are “inherent risk” and “residual risk.” How you define these concepts also determines the results of your risk analysis, measurement, and, eventually, the risk-based allocation of your resources as a country, agency, or financial institution, which indeed is the main point of a risk-based approach.
There is no doubt that risk –particularly money laundering and terrorist financing risk- is quite a complex phenomenon, and we need to be very cautious about relying on quasi-scientific approaches in its analysis. However, some formulations, approximations, and assumptions for risk modeling are practical needs and being used by policymakers, supervisors, and the private sector. Notwithstanding that relevant data is still in its infancy and yet to support very scientific and empirical modeling, the existing models should at least be clear, logical, and internally consistent as a starting point.
In the Oxford English Dictionary, “inherent” and “residual” are defined as follows:
- Inherent: Existing in something as a permanent attribute or quality; forming an element, esp. a characteristic or essential element of something; belonging to the intrinsic nature of that which is spoken of; indwelling, intrinsic, essential.
- Residual: Remaining; still left; left over; (also) of or relating to a residue (general). Resulting from or expressing the subtraction of one quantity from another (mathematics).
In some projects I have led or participated in recently, we have defined residual ML/TF risk as the remaining risk after assessing inherent risks and accounting for the impact of AML/CFT controls. Essentially, the inherent ML/TF risk of a client, transaction, or business line is the default risk level without any AML/CFT controls. As AML/CFT controls are applied and their effectiveness increases, the overall risk level decreases below the inherent risk level, resulting in the “residual risk.” This definition, which is both intuitive and based on feedback from various tests and pilot implementations of risk assessment tools, has consistently produced logical results compared to other formulations we tried.
Recently, the FATF published its new guidance for National Money Laundering Risk Assessments. It defines inherent risk as the “level of risk that exists before introducing any mitigating measures” and residual risk as “the level of risk that remains after risk mitigation measures have been introduced.” According to the guidance, residual risk is lower than or at most equal to the inherent risk, depending on the quality of the controls implemented. This aligns closely with our interpretation of inherent and residual risk above. However, it is important to note that FATF Recommendations themselves, which are principle-based, do not define these concepts -which I believe is the right approach-. FATF’s guidance papers, including this one, are not part of the standards and are not binding.
As I tried to explain above, my view is that, by definition, a residual risk cannot exceed the inherent risk, and would be lower, or as a maximum, equal to the inherent risk level. Although there is a common understanding that residual risk is a function of inherent risk and AML controls, which can be represented as RR = f {RI, CAML}, not all agree about the exact formula in this equation. Let’s make this question clearer with an illustration below:
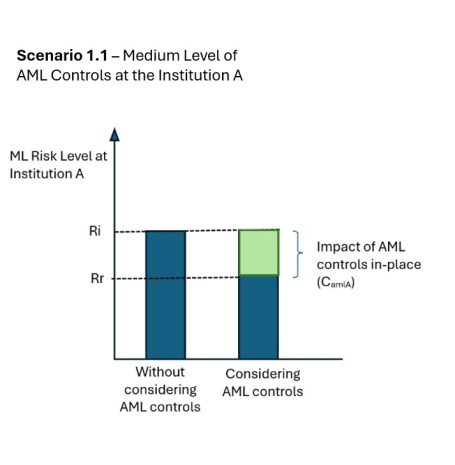
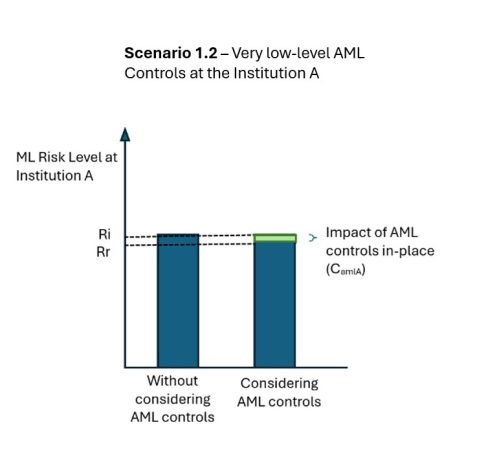
Approach 1 to Residual Risk: Subtracting AML Controls
RR = {RI - CAML}
RR = residual risk, RI =inherent risk, CAML = the impact of AML controls.
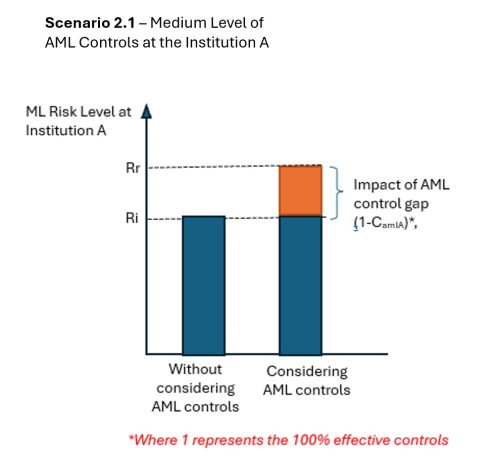
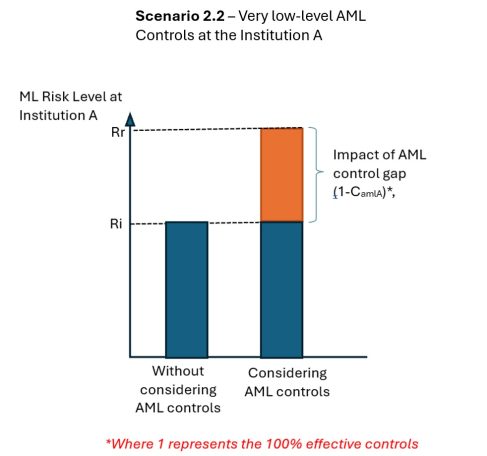
Approach 2 to Residual Risk: Weighting AML Control Gap
RR ={w1 RI + w2 (1- CAML)}
RR = residual risk, RI =inherent risk, CAML = the impact of AML controls, 1-CAML = the AML control gap, w1 = the weight assigned to inherent risk, w2 = the weight assigned to AML control gap.
I hope this example clarifies the question. In Approach 1, the residual risk cannot exceed the inherent risk level, whereas in Approach 2, it can be much higher depending on the weight assigned to the control gap. In other words, Approach 2 penalizes the lack of AML controls in the overall risk score. Although I prefer Approach 1, I have observed that many institutions and agencies frequently use Approach 2.
Indeed, both approaches have their own assumptions and underlying justifications. The problem discussed above may be partially addressed by using a more appropriate term rather than “residual risk” in the second approach. For example, instead of residual risk, it may be more intuitive to call it an “overall risk” or “composite risk”. However, the question is not only about the reasonableness of the term but also relates to the substance of risk understanding.
In the next step of the discussion, based on a practical example, we will continue to discuss the pros and cons of these two approaches. However, for a blog, it is the right time to pause and hear your views and feedback.
Here are some other topics I am planning to cover in the next blogs in this series:
- Inherent vs. residual risk: Practical implications.
- How to define ML/TF risk? Can we reconcile the definitions of FATF and ISO?
- The question of assessing consequences: Challenges and possible solutions.
- How ML/TF risks differ from other financial and operational risks in an institution.
- How risk-based are FATF assessments themselves?
Let me know your views and feedback.
©Copyright. All rights reserved.
We need your consent to load the translations
We use a third-party service to translate the website content that may collect data about your activity. Please review the details in the privacy policy and accept the service to view the translations.